What is the product of 6 x 7? Did you know it instantly? Did you automatically think 42? Teachers in grades 3-6 spend substantial energy and time helping students to know facts like this automatically. How often have you heard, “if my students just knew their multiplication facts…”? Maybe you have even said this yourself. When students lack quick recall of their basic facts, they seem to struggle so much more than their peers. There is little debate regarding the importance of having quick recall of basic facts. What is often up for debate is what to do about the students who continue to struggle to learn their basic facts (Sawchuk, 2023).
The solution to this dilemma is The Fact Tactics™ Fluency Program. This twenty-week, step-by-step, tested program “will transcend recall of basic facts and increase student access to mathematics proficiency, providing a gateway to increased success with mathematics for each and every learner” (Dixon, 2023, p. 6). According to Ms. Keyes, an assistant principal in a school that used this program, it is “intentional and easily accessible for teachers and highly engaging for students.”
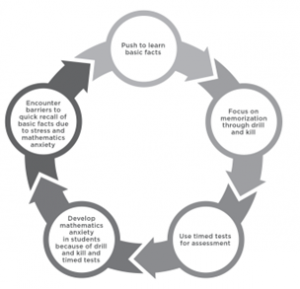
Schools and districts spend considerable resources on programs that require students to practice their basic facts using techniques such as computer applications and traditional flash cards. There are often rewards for students who can “beat the clock” and multiply a set number of facts within a given time limit. But at what cost? How much of the anxiety students experience about mathematics can be attributed to these time-pressured experiences? “Evidence strongly suggests that timed tests cause the early onset of math anxiety for students across the achievement range” (Boaler, 2014, p. 469). The resulting mathematics anxiety often serves as a gatekeeper to students pursuing mathematics-related careers. Furthermore, if these techniques are successful, why do we need to focus on basic facts with the same students year after year after year? Figure 1 describes this perpetual cycle.
Figure 1: Typical cycle for basic facts instruction (Dixon, 2023, p. x).
These efforts are not providing acceptable results. We know students need practice, but how and when should that be accomplished? We know that we need to assess where students are with their facts, but how can we avoid causing anxiety in our students who struggle to develop their knowledge of the facts? This is a topic I’ve explored for many years. Figure 2 provides an overview of the program that is the answer to these questions. The twenty-week program is described in detail in The Fact Tactics™ Fluency Program: Building Reasoning Skills for Multiplication in Grades 3-6 (Dixon, 2023). This model contrasts with the typical cycle described earlier.
Figure 2: The Fact Tactics Fluency Program pathway (Dixon, 2023, p. xx).
Let’s return to 6 x 7. If you could not recall the product of 6 x 7 automatically, would you be more successful recalling that 3 x 7 is 21? The answer is likely yes. Can you double 21 without much effort? Also, yes. Determining the product of 6 x 7 by thinking 3 x 7 and double is not automatic recall, but it is quick recall. You can probably think of other ways that you could determine the product of 6 x 7 that go beyond memorization (see Figure 3 for a web of ideas).
Figure 3: Strategies for determining the product of 6 x 7.
In some cases, thinking about facts using strategies is as important as automatic recall. The thinking involved in using strategies like this helps students to develop a deeper understanding of mathematics in general and multiplicative reasoning in particular. This sort of understanding is a prerequisite to success with later mathematics, including algebra. Readiness for algebra requires “a grasp of the meaning of the basic operations of addition, subtraction, multiplication, and division. It must also include use of the commutative, associative, and distributive properties; computational facility; and the knowledge of how to apply the operations to problem-solving” (National Mathematics Advisory Panel, 2008, p. 17). Thinking 6 x 7 is 3 x 7 and double is an application of the associative property of multiplication, as follows:
6 x 7 = (2 x 3) x 7 = 2 x (3 x 7).
You might have derived the product of 6 x 7 by thinking 5 x 7 add 7. This is an application of the distributive property of multiplication over addition, as follows: 6 x 7 = (5 + 1) x 7 = (5 x 7) = (1 x 7) = (5 x 7) + 7.
What is essential is that students have access to strategies that make sense to them and that they can use these strategies flexibly, accurately, efficiently, and appropriately, which is the meaning of procedural fluency according to Adding It Up (National Research Council, 2001). When supporting students to learn their basic multiplication facts, strategies based on multiplicative reasoning should be emphasized for each and every student. Direct modeling or counting strategies such as drawing an array or using repeated addition to determine the product of a fact do not rely on multiplicative reasoning but rather additive reasoning. These types of experiences are necessary for developing an understanding of multiplication but become counterproductive if students remain in this space.
Students should be encouraged to use strategies based on the application of properties of operations to determine the products of facts they don’t know such as those shared for determining the product of 6 x 7. Practice applying properties of operations helps students to develop strong links between strategies and different facts. Students can be assessed on their fluency with basic facts using self-assessment where students determine whether they know products of facts or if they are relying on strategies to determine them. These assessments can be shared with the teacher to guide further practice without creating the mathematics anxiety caused by timed tests.
This journey towards fluency is so important in preparing for algebra that students who already know their basic facts should be provided with tasks that will allow them to apply properties of operations as well. Consider how you would determine the product of 4 x 42 using mental computation. What strategies could you use? You could think 4 x 40 is 160 add 4 x 2 or 8, but you might also think 2 x 42 is 84 and double. Symbolically, these strategies are represented as follows:
4 X 42 = 4 x (40 + 2) = (4 x 40) = (4 x 2), and
4 x 42 = (2 x 2) x 42 = 2 x (2 x 42).
Both are strategies grounded in the properties of operations (the distributive property of multiplication over addition and the associative property of multiplication). Tasks like these afford learners who need more challenge an opportunity to apply properties of operations to problems beyond basic facts.
When facts are introduced in a strategic order, and teachers support students to use and practice strategies based on multiplicative reasoning to determine the products, students develop quick recall of basic facts and an understanding of the properties of operations. It is about being fact-tactical.
The Fact Tactics Fluency Program “is a brilliant program that our teachers and students love! The order of facts and the specific embedded strategies help students make sense of multiplication, and it provides prerequisite learning for a variety of standards. Our students have definitely improved in multiplication and are making connections across other math domains.”
Melissa Logsdon, Numeracy Coach, Robertson County Schools
About the author: Juli K. Dixon, PhD, is a professor of mathematics education at the University of Central Florida. An active researcher, she has also taught mathematics at the elementary, middle, and secondary levels.